그래프(Graph)란?
그래프란 사물이나 개념 간의 연결 관계를 표현해주는 자료구조의 일종이다.
예를 들면 SNS에서 친구와 친구 사이의 관계라던지 도로의 교통망, 웹사이트 간의 링크 등과 같이 어떤 요소와 요소간의 관계를 나타낼 때 주로 사용할 수 있다.
그래프는 어디에 활용할 수 있을까?
- 철도, 도로 등 교통망 분석: 어떤 교통망을 이용해야 최소 비용/최단 거리/최소 시간 내에 이동할 수 있는가?
- SNS 분석: 친구 관계 분석 및 친밀도 분석
- 인터넷 망 분석: 어떤 라우터로 가야 최대한 빨리, 최소 비용, 최소 전송 용량으로 전송할 수 있는가?
- 한 붓 그리기: 그래프 탐색을 통해 단순 사이클을 생각해보면 한 붓 그리기 문제를 해결할 수 있다.
이 외에도 현실세계의 다양한 모델에 그래프 이론을 활용하면, 여러 가지 문제를 쉽게 해결할 수 있습니다.
현실세계에 다양하게 적용할 수 있는 만큼 그래프 이론이 중요하다는,,
그래프의 정의
그래프 G(V, E)는 정점(Node, Vertex)과 간선(Edge)들로 구성되어 있다.
따라서 그래프를 정의할 때는 정점의 위치나 간선의 순서(방향과는 다른 말이다) 등은 고려하지 않고 오로지 정점과 정점간의 관계로만 정의된다.
그렇기 때문에 아래의 두 그래프는 모양은 다르지만 같은 그래프로 정의될 수 있다.
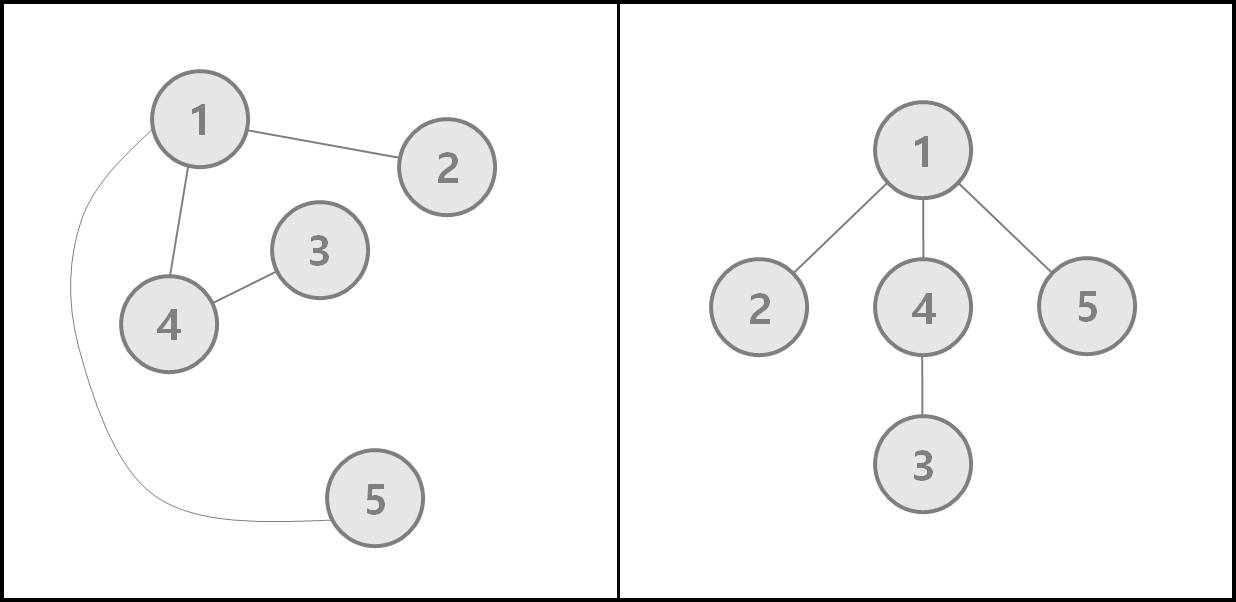
한 정점에 연결되어 있는 간선의 개수를 차수(Degree)라고 한다.
위 그래프에서는 1의 차수는 3, 4의 차수는 2, 3의 차수는 1이다.
그래프의 종류, 용어
그래프는 단순하게는 위와 같이 정점과 간선만으로 나타낼 수 있지만, 표현하고자 하는 바에 따라서 다양한 종류의 그래프가 존재한다.
그 중 대표적인 몇 가지 것들만 살펴보도록 하겠다.
1. 방향 그래프(유향 그래프, directed graph) / 무방향 그래프(무향 그래프, undirected graph)
방향 그래프는 그래프의 간선에 방향이라는 속성이 추가된 그래프이다.
위의 그래프에 방향을 추가하여 방향 그래프로 만들어보자.
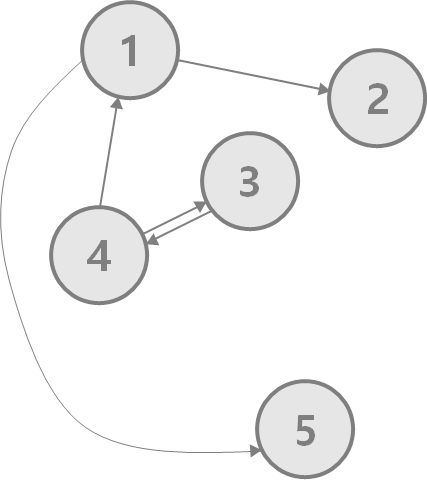
무방향 그래프의 경우에는 1-2 사이에 연결된 간선이 양쪽의 간선을 모두 연결하고 있지만, 방향 그래프의 경우에는 두 정점 사이의 간선이 존재하더라도 방향 때문에 2>1로 갈 수 없다.
방향이 없는 그래프에서는 한 간선이 서로 다른 방향의 두 간선을 의미한다고 생각하면 된다.
방향 그래프와 무방향 그래프의 차이는 인스타그램과 페이스북의 예시를 통해 알 수 있다.
인스타그램의 경우 팔로잉, 팔로워라는 개념으로 팔로잉을 하더라도 맞팔로잉을 하지 않으면 팔로워가 되지 않기 때문에 친구 관계가 방향 그래프의 형태로 구성되게 된다. 서로 맞팔로잉을 하는 경우가 정점 3,4와의 관계일 것이다.
하지만 페이스북의 경우에는 친구신청을 수락하면 서로 친구를 맺는 관계로, 한쪽만 친구를 맺는 관계가 형성될 수 없기 때문에 무방향 그래프와 같이 구성된다.
그 외에도 방향 그래프의 현실에서의 예시로는 일방통행 도로나 짝사랑 등이 있다.
2. 가중치 그래프(weighted graph)
가중치 그래프는 간선에 가중치라는 속성이 추가된 그래프이다. 가중치란 한 정점에서 다른 정점으로 이동하는데 필요한 거리, 시간, 비용 등을 의미한다.
방향, 무향 상관 없이 가중치 그래프가 될 수 있다.
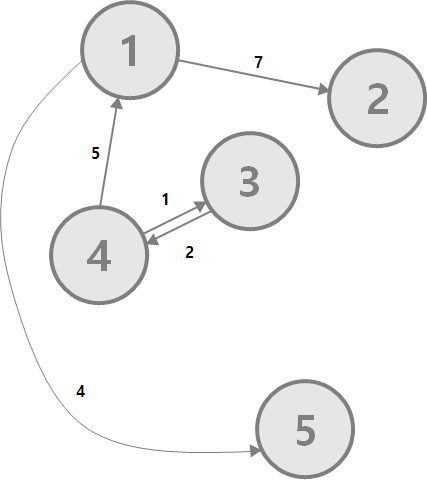
두 장소 사이의 거리나 이동하는데 걸리는 시간, 이동 비용, 사람 사이의 호감도 등 그래프의 다양한 정보들을 표현할 수 있다.
3. 다중 그래프(multigraph) / 단순 그래프(simple graph)
두 정점 사이에 간선이 두 개 이상 있는 그래프를 다중 그래프라고 한다. 반대로 두 정점 사이에 한 개의 간선만 가지는 경우를 단순 그래프라고 한다.
다중 그래프의 간선을 Multiple Edge라고 부르며, 각각의 간선들은 서로 다른 간선이다.
가중치가 있는 경우 각각의 간선이 다른 가중치를 가질 수 있다.
n차선 도로와 같은 모델에서 다중 그래프를 활용할 수 있다.
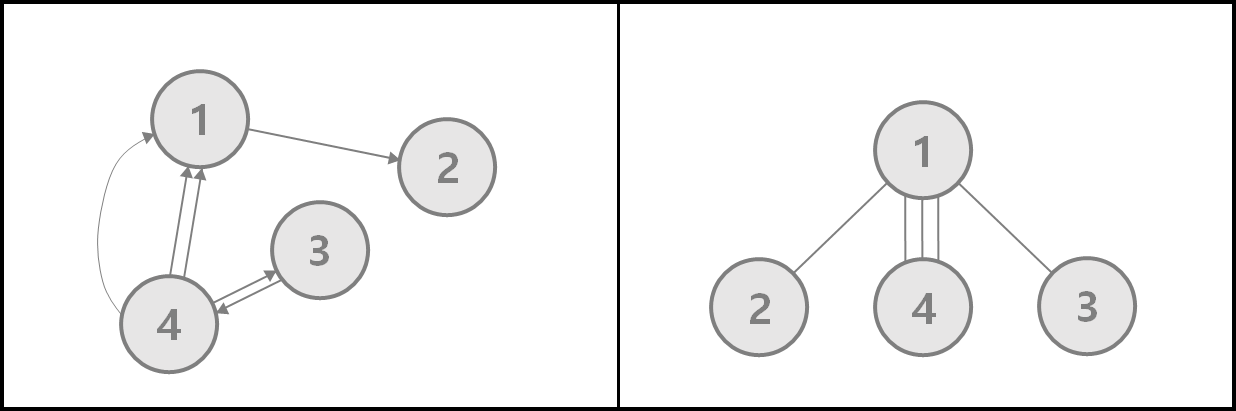
4. 루프(Loop)
한 정점에서 출발해서 같은 정점으로 가는 간선이 있을 경우, 이를 루프라고 한다.

5. 경로(Path)와 사이클(Cycle)
그래프에서의 경로란 하나의 정점에서 다른 정점까지 가는 경로를 의미한다.

위 그래프의 경우, 정점1에서 정점4로 이동하는 경로로는 1-2-4, 1-3-4, 1-2-5-4가 있다.
사이클은 한 정점에서 출발하여, 같은 정점으로 돌아오는 경로를 뜻한다.
1에서 출하여 1로 돌아오는 사이클로는 1-2-4-1, 1-3-4-1, 1-2-5-4-1이 있다.
예시로 들었던 경로, 사이클과 같이 한 번 방문했던 정점을 다시 방문하지 않는 경로/사이클을 단순 경로/단순 사이클이라고 부른다. 그래프 이론에서 특별한 말이 없는 경우에 경로나 사이클을 구하라고 한다면 단순 경로/단순 사이클이라고 생각하면 된다.
단순 사이클이 아닌 예시를 들어보면, 1-2-5-2-4-1이 있다.
그래프의 표현
그래프는 인접 행렬, 인접 리스트로 표현할 수 있다.
1. 인접 행렬
인접 행렬이란, 정점의 연결 관계를 행렬을 통해 표현하는 방식이다.
한 정점과 다른 정점이 연결되어있을 경우 행렬에 1(true)을, 아닐 경우 0(false)을 저장한다.
가중치가 있는 경우에는 1 대신 가중치 값을 저장해줄 수 있고, 방향이 있는 경우에는 한 쪽 방향에만 true로 저장해주면 된다.
N개의 정점이 있다고 가정하면 N개의 정점에 각 N개의 정점의 연결 관계를 저장해주어야 하기 때문에, N*N 크기의 저장 공간이 필요하다.

코드를 통해 구현할 경우에는 N*N 크기의 이차원 배열을 만들어서 다음과 같이 구현해줄 수 있다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = 5;
int[][] adj = new int[n + 1][n + 1];
StringTokenizer st;
while ((st = new StringTokenizer(br.readLine())).hasMoreElements()) {
// 연결 관계가 주어진다.
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
// 무방향 리스트이기 때문에 양쪽의 연결 관계를 바꿔준다.
adj[a][b] = 1;
adj[b][a] = 1;
}
// 인접행렬 출력
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
System.out.print(adj[i][j] + " ");
}
System.out.println();
}
}
}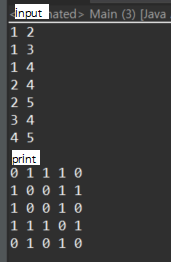
인접행렬 장점 : 두 정점의 인덱스만 있다면 별다른 연산을 거치지 않아도 배열의 인덱스를 통해 두 정점간의 연결 관계를 바로 확인할 수 있다.
인접행렬 단점: 그래프의 간선의 개수에 상관없이 정점의 수가 N개라면 N^2 크기의 공간을 차지한다는 것이다.
2. 인접 리스트
인접 리스트는 각 정점마다 연결 된 간선의 정보를 리스트를 이용하여 저장하는 방식이다.
그래프의 정점이 N개라고 하더라도, 정점마다 연결된 간선의 개수는 몇 개인지 알 수 없다. 따라서 한 정점과 간선을 통해 연결되어있는 정점을 리스트로 저장하는 것이다.
Java의 경우 ArrayList를 통해 구현할 수 있다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = 5;
ArrayList<Integer>[] adj = new ArrayList[n + 1];
for (int i = 1; i <= 5; i++)
adj[i] = new ArrayList<Integer>();
StringTokenizer st;
while ((st = new StringTokenizer(br.readLine())).hasMoreElements()) {
// 연결 관계가 주어진다.
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
// 무방향 리스트이기 때문에 양쪽의 연결 관계를 바꿔준다.
adj[a].add(b);
adj[b].add(a);
}
// 인접행렬 출력
for (int i = 1; i <= n; i++) {
System.out.print("adj[" + i + "] : ");
for (int j = 0; j < adj[i].size(); j++) {
System.out.print(adj[i].get(j) + " ");
}
System.out.println();
}
}
}
위와 같이 한 정점과 연결된 정점들의 모든 정보가 저장되는 것을 볼 수 있다.
그렇다면 인접 리스트에서 가중치나 추가 정보를 저장하려면 어떻게 해야 할까?
> 구조체를 사용하거나, Java의 경우는 클래스를 추가로 만들어서 ArrayList의 타입을 해당 클래스로 지정해주어, 조금 더 다양한 정보의 표현이 가능합니다.
인접 리스트의 경우 인접행렬과는 다르게 공간의 크기를 정점과 간선의 갯수인 V+E만큼밖에 차지하지 않습니다.
그리고 한 정점과 연결되어있는 모든 간선을 찾는 데 걸리는 시간 또한 인접 행렬은 V인데 반해, 인접 리스트는 그 정점의 간선의 갯수만큼밖에 걸리지 않습니다. 이는 항상 정점의 갯수인 V보다 작기 때문에 시간과 공간 면에서 인접 리스트가 유리하고, 그렇기 때문에 그래프 문제를 해결할 때 대부분의 경우에는 인접 리스트를 사용합니다.
다만 아래의 문제 예시같은 경우에는 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하라는 조건 때문에 인접 리스트를 사용할 경우 정렬 등의 추가 작업이 필요하게 되어서, 인접 행렬을 사용하는게 더 빠르더라는,,,
https://www.acmicpc.net/problem/1260
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net
'알고리즘 > 자료구조' 카테고리의 다른 글
| 트라이(Trie)의 개념과 활용 (0) | 2022.02.15 |
|---|---|
| 그래프의 탐색(DFS, BFS) (0) | 2021.09.02 |
| HashMap에 대해서 알아보자 (0) | 2021.08.23 |
| 비트마스크(BitMask)에 대해서 알아보자 (0) | 2021.08.08 |
| [자료구조] 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2021.08.07 |