트라이(Trie)란?
트라이는 문자열을 효율적으로 검색하기 위해 고안된 Search Tree의 일종입니다.
어떠한 알고리즘을 이용하여 정수나 실수 등과 같은 기본 자료형의 변수를 비교할 때에는 각 자료마다 동일한 시간이 걸릴 것이지만, 문자열의 경우 각각의 문자열마다 길이가 다르기 때문에 동일한 알고리즘으로 비교하더라도 같은 시간이 걸린다고 말할 수 없습니다. 최악의 경우 문자열의 길이만큼의 시간이 더 걸리게 될 것입니다.
BST를 이용한 검색
(1) 정수 자료형의 경우
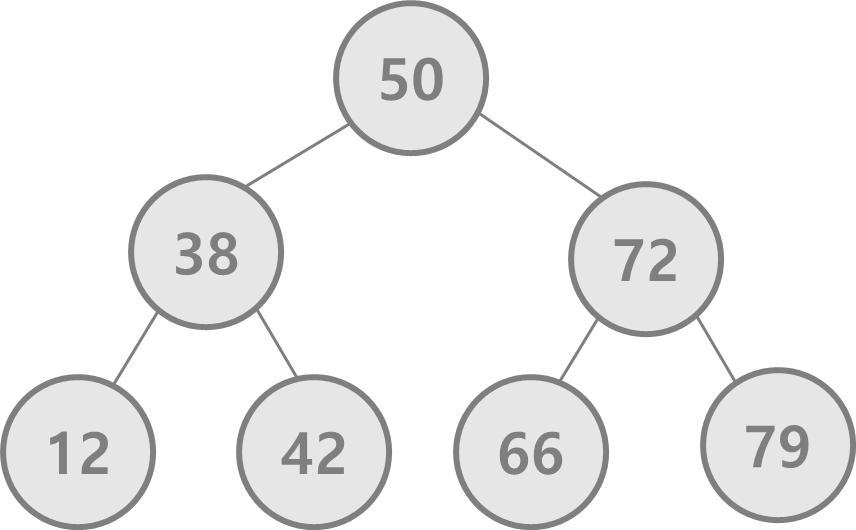
한 번의 검색마다 트리의 깊이가 1씩 깊어집니다.
트리의 깊이가 1씩 깊어질 때마다 비교해야 할 자료형은 절반씩 줄어들기 때문에 총 검색의 시간복잡도는
O(logN) 일 것입니다.
(2) 문자열의 경우
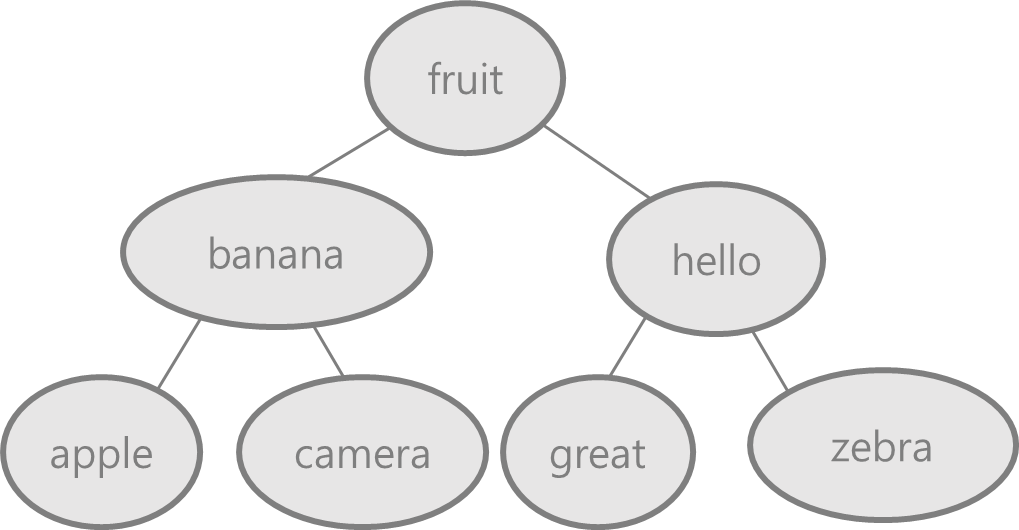
한 번 검색마다 트리의 깊이가 1씩 깊어집니다.
하지만 문자열이 같은지 비교하려면 문자열의 길이만큼 비교해줘야 할 것입니다.
문자열의 최대 길이를 M이라고 한다면 총 시간복잡도는 O(MlogN)이 될 것입니다.
하지만 트라이를 이용한다면 O(M)만에 할 수 있습니다.
어떻게 이렇게 할 수 있을지 알아봅시다.
TRIE
1. TRIE의 구조
우선 TRIE가 어떤 식으로 구성되어있는지부터 살펴보자.
만약 문자열 집합 S에
S = { "hi", "high", "tea", "ten", "he", "be" }
가 들어있다고 하자. 그러면 TRIE는 아래와 같이 구성된다.

색깔이 다르게 표시된 부분은 글자가 끝났음을 표시해준 end node인 부분이다.
이런식으로 문자열을 탐색한다면 속도도 굉장히 빠르고, 만약 te까지 검색했다면 tea, ten을 완성할 수 있다는 사실을 알 수 있기 때문에 검색어 자동완성 등에 활용할 수 있다.
시간복잡도
제일 긴 문자열의 길이: L, 총 문자열의 수: M
생성시 시간복잡도: O(M*L)
삽입: O(L)
탐색시 시간복잡도: O(L)
위와 같이 탐색의 시간복잡도는 매우 짧음을 알 수 있다.
하지만 노드에서 자식들에 대한 포인터들을 맵으로 저장한다는 점에서 저장 공간의 크기가 크다는 단점이 있다.
2. TRIE의 구현
위에서 살펴본 TRIE의 구조 그대로 구현해보도록 하겠다.
각각의 노드 정보와 트라이 정보가 필요할 것이다.
(1) Node
각각의 노드는 현재의 문자열 정보(Character 값)과 다음 노드에 대한 정보가 필요하다.
또한 문자열이 끝났는지 저장해줄 값도 필요하다.
class Node {
// child Node
Map<Character, Node> childNode = new HashMap<>();
// 마지막 글자 여부
boolean end;
}
(2) Trie
구현한 노드를 바탕으로 트라이를 구성한다.
(2)-1. 문자열 삽입
루트 노드에서 시작하여 진행한다.
만약 다음 문자열에 해당하는 문자열이 이미 존재한다면 해당 노드로 간다.
그렇지 않다면 새로운 노드를 만들어서 해당 노드로 가준다. (약간 LinkedList 구현하는 느낌)
예를들어 hi를 넣은 후에 high를 넣는 경우 hi까지는 기존에 넣어놨던 hi를 타고 가면 되지만, gh의 경우 새로운 노드를 만들어서 진행해야 할 것이다.
코드로는 다음과 같이 구현할 수 있다.
void insert(String str) {
Node node = this.root;
for (int i = 0; i < str.length(); i++)
node = node.childNode.computeIfAbsent(str.charAt(i), key -> new Node());
node.end = true;
}computeIfAbsent() 등과 같이 Map Interface의 메서드들에 대해서는 아래 블로그를 참고하였다.
정리를 굉장히 잘 해주셨음
https://codingnojam.tistory.com/39
[Java] Map Interface의 유용한 메서드를 알아보자! (Java 8 기준)
안녕하세요 코딩노잼입니다. 오늘은 Map Interface의 메서드 중 Java8에서 등장한 유용한 메서드들을 알아보겠습니다. Java8 하면 빼놓을 수 없는 게 람다식인데 오늘 알아볼 메서드들은 대부분 람다
codingnojam.tistory.com
(2)-2. 문자열 검색
루트 노드에서 시작하여 진행한다.
만약 다음 검색할 문자를 찾지 못하면 노드를 null로 바꿔준다.
검색할 문자열을 다 진행하기 전에 노드가 null이 되면 찾지 못함: return false
검색을 마치면 true를 return
boolean search(String str) {
// root Node에서 시작
Node node = this.root;
for (int i = 0; i < str.length(); i++) {
node = node.childNode.getOrDefault(str.charAt(i), null);
if (node == null)
return false;
}
return true;
}
그러면 삽입, 검색 기능을 가진 TRIE의 구현이 완료되었다!!
<전체 소스코드>
class Trie {
Node root = new Node();
void insert(String str) {
Node node = this.root;
for (int i = 0; i < str.length(); i++)
node = node.childNode.computeIfAbsent(str.charAt(i), key -> new Node());
node.end = true;
}
boolean search(String str) {
// root Node에서 시작
Node node = this.root;
for (int i = 0; i < str.length(); i++) {
node = node.childNode.getOrDefault(str.charAt(i), null);
if (node == null)
return false;
}
return true;
}
}
class Node {
Map<Character, Node> childNode = new HashMap<>();
boolean end;
}
요 TRIE를 가지고 몇 가지의 응용 문제들을 풀 수 있다.
1. https://www.acmicpc.net/problem/14426
14426번: 접두사 찾기
문자열 S의 접두사란 S의 가장 앞에서부터 부분 문자열을 의미한다. 예를 들어, S = "codeplus"의 접두사는 "code", "co", "codepl", "codeplus"가 있고, "plus", "s", "cude", "crud"는 접두사가 아니다. 총 N개의 문자
www.acmicpc.net
위의 내용을 잘 이해했다면 쉽게 해결 가능할 것이다.
2. https://www.acmicpc.net/problem/5052
5052번: 전화번호 목록
첫째 줄에 테스트 케이스의 개수 t가 주어진다. (1 ≤ t ≤ 50) 각 테스트 케이스의 첫째 줄에는 전화번호의 수 n이 주어진다. (1 ≤ n ≤ 10000) 다음 n개의 줄에는 목록에 포함되어 있는 전화번호가
www.acmicpc.net
이 문제는 트라이를 쪼금 응용하면 풀 수 있는데, 트라이의 구조를 이해하는데 도움이 되는 문제이다.
스스로 풀어보는 것을 추천하며, 풀이가 궁금하다면 아래 링크 참조
https://kkap999.tistory.com/72
참고 도서: [구종만, 인사이트] 프로그래밍 대회에서 배우는 알고리즘 문제해결전략2
참고 링크: https://www.youtube.com/watch?v=WooOuXIiRjE
https://twpower.github.io/187-trie-concept-and-basic-problem
'알고리즘 > 자료구조' 카테고리의 다른 글
| Comparable과 Comparator (2) | 2025.08.29 |
|---|---|
| 그래프의 탐색(DFS, BFS) (0) | 2021.09.02 |
| 그래프에 대해서 알아보자 (0) | 2021.09.02 |
| HashMap에 대해서 알아보자 (0) | 2021.08.23 |
| 비트마스크(BitMask)에 대해서 알아보자 (0) | 2021.08.08 |